Command manual

This is a ceramic model with different failure mechanisms in compression and tension. The material is assumed to have a pressure dependent shear resistance. At positive pressures, plastic flow is a combination of shearing and dilatation. Inelastic dilatation is interpreted as crushing that gradually reduces the shear resistance of the material. A brittle fracture criterion combined with node splitting is used on the tensile side. Note that node splitting can not occur in MERGE or REFINE interfaces.

For positive pressures the yield function $\Phi$ is defined as:

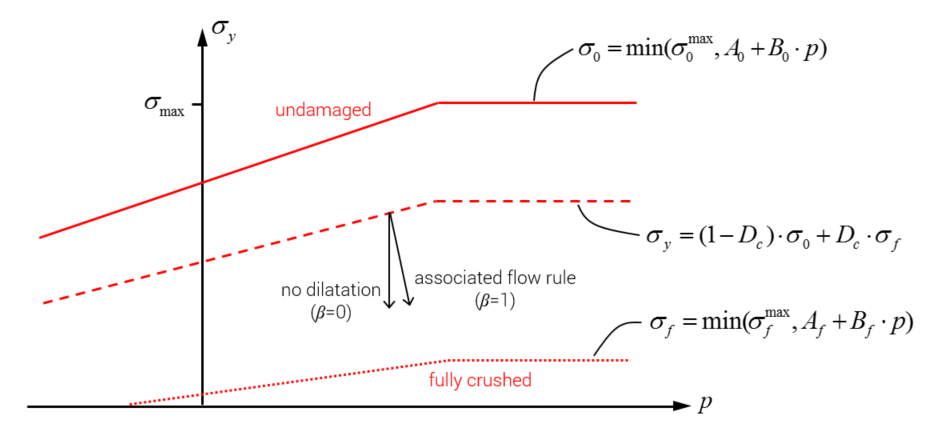
$\Phi = \sigma_{eff} - \sigma_0 \cdot (1-D_c) - \sigma_f \cdot D_c$

where:

$\sigma_0 = \mathrm{min} (\sigma_0^{max}, A_0 + B_0 \cdot p)$

$\sigma_f = \mathrm{min} (\sigma_f^{max}, A_f + B_f \cdot p)$

Further, $\sigma_{eff}$ is the effective von Mises stress, $p$ is the pressure and $D_c$ is a crushing damage parameter ranging from 0 to 1. The inelastic flow direction is defined as:

$\dot \varepsilon_{vol}^p = \beta \dot\lambda \displaystyle{ \frac{\partial \Phi}{\partial p} }$

$\dot \varepsilon_{dev}^p = \dot\lambda \displaystyle{ \frac{\partial \Phi}{\partial \sigma_{eff}} }$

Here $\varepsilon_{vol}^p$ is a volumetric crushing strain and $\varepsilon_{dev}^p$ is a deviatoric inelastic shear strain. $0 \lt \beta \leq 1$ is controlling the amount of volumetric dilatation during plastic flow.

$D_c = \mathrm{min}(1, \displaystyle{ \frac{\varepsilon_{dev}^p}{\varepsilon_f} })$

In addition there is a brittle spall criterion. Cracks initiate once a spall damage parameter, $D_s$, has evolved from 0 to 1.

$\dot D_s = \left\{ \begin{array}{cc} \displaystyle{\frac{1}{t_s} \cdot ( \frac{\sigma_1}{\sigma_s (1 - D_c)(1 - D_0)} )^{\alpha_s}} & \sigma_1 \geq \sigma_s (1 - D_c) (1 - D_0)\\ 0 & \sigma_1 \lt \sigma_s (1 - D_c) (1 - D_0) \end{array} \right. $

where $\sigma_1$ is the maximum principal stress and $\sigma_s$ is the spall stress of undamaged material.

$D_0$ is an optional initial defect (damage) value that can be defined through INITIAL_DAMAGE_RANDOM or INITIAL_DAMAGE_SURFACE_RANDOM. Accounting for initial defects is essential for a physically realistic behavior of many brittle materials. It is generally more important when dealing with relatively small material volumes.

Crack propagation is optionally controlled by a stress intensity criterion. The stress intensity $K_I$ is estimated for the integration points surrounding the crack tip. The crack will propagate if $K_I > K_c$ (Modus I crack).

The pressure-volume relationship is cubic in compression:

$p = K_1 ( \mu + \varepsilon_{vol}^p ) + K_2 \mu^2 + K_3 \mu^3 \;\;\; \mu > 0$

and linear in tension:

$p = K_1 ( \mu + \varepsilon_{vol}^p ) \;\;\; \mu \lt 0$

where:

$\mu = \rho/\rho_0 - 1$

Yield stress as a function of pressure and damage