MAT_EXPLOSIVE_JWL
FE
CFD
Material properties
"Optional title"
mid, $\rho_0$, $E$, $\nu$
$\sigma_0$, $Q$, $C$, $S$, $\Gamma$
$A$, $B$, $R_1$, $R_2$, $\omega$, $e_0$, $D$, $t_b$
Parameter definition
Description
This is a model for explosive materials. It is currently implemented for Finite Elements and CFD. However, only the Finite Element version uses the undetonated properties. The pressure in the undetonated material is defines as:
$\displaystyle{ p = \frac{K \eta}{(1-S \eta)^2} \cdot \left( 1 - \frac{\Gamma \eta}{2} \right) + \Gamma \rho_0 e }$
$\displaystyle{ \eta = 1 - \rho_0 / \rho }$
where $K$ is the bulk modulus, $\rho_0$ is the initial density and $\rho$ is the current density. Undetonated material is treated as elasto-plastic with a (J2) flow stress, according to:
$\displaystyle{\sigma_y = \sigma_0 + Q \left( 1 - \mathrm{exp} (-C \varepsilon_p)\right)}$
At detonation the chemical energy $e_0$ is released and all shear stresses are set to $0$. The pressure $p$ is defined accoding to the JWL equation-of-state:
$\displaystyle{ p = A \left( 1 - \frac{\omega}{R_1 V} \right) \mathrm{e}^{-R_1 V} + B \left( 1 - \frac{\omega}{R_2 V} \right) \mathrm{e}^{-R_2 V} + \omega e}$
where $V$ is the relative volume:
$\displaystyle{ V = \rho_0 / \rho}$
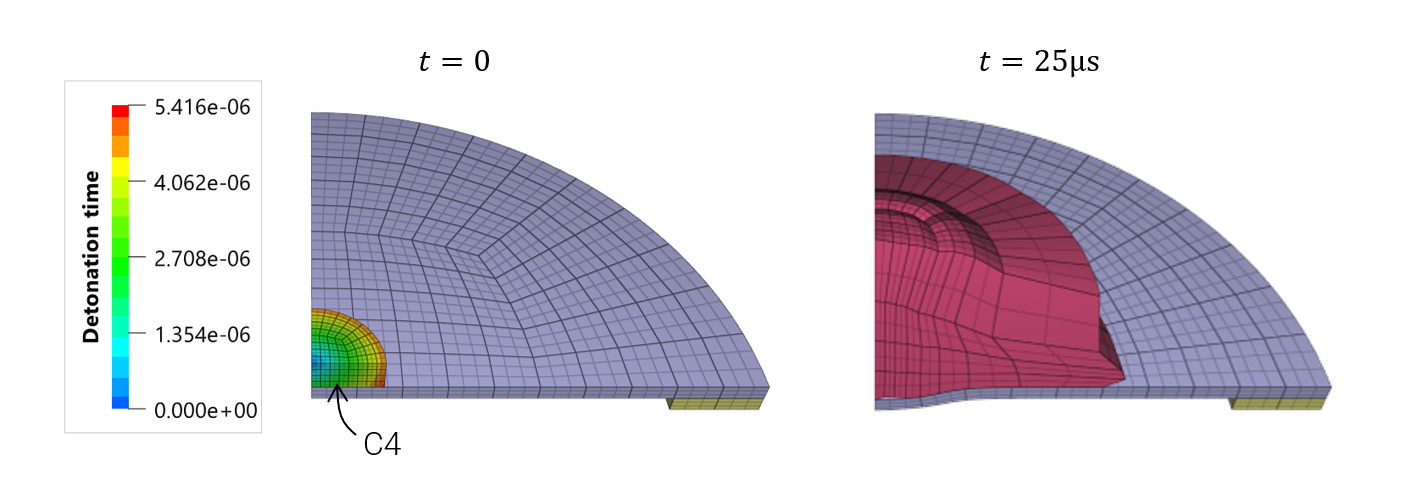
The model uses a programmed burn assumption and at least one detonation point must be defined with the command DETONATION.
Example
Contact detonation
A C4 charge modelled with Finite Elements and MAT_EXPLOSIVE_JWL. Quadratic elements are well-suited for this purpose, if combined with the command LOAD_ELEMENT_SMOOTHING. The smoothing command is essential for mitigating spurious high-frequency oscillations on element level. A programmed burn approach is employed, with the ignition point defined using the command DETONATION.